参考:Keras Documentation, Keras Github, Keras文档, 卷积神经网络, 机器学习, Images Datasets, Deep Learning Papers, Deep Learning with keras, Deep Learning step-by-step
本文使用keras和tensorflow构建神经网络。
$ pip install keras
$ pip install tensorflow
$ python
>>> import os
>>> os.environ['KERAS_BACKENG']='tensorflow'
Using TensorFlow backend.
也可以使用Theano作为backend。
[TOP]
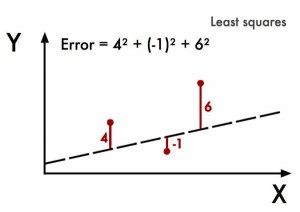
1805年,法国数学家勒让德(Adrien-Marie Legendre)发表了《计算彗星轨道的新方法》,提出了最小二乘法。
# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, coordinates):
totalError = 0
for i in range(0, len(coordinates)):
x = coordinates[i][0]
y = coordinates[i][1]
totalError += (y - (m * x + b)) ** 2
return totalError / float(len(coordinates))
# example
compute_error_for_line_given_points(1, 2, [[3,6],[6,9],[12,18]])

通过修改m和b,使预测值\((m*x+b)\)和实际值\(y\)的误差平方和逐渐减小。这其中已经包含了机器学习的核心思想:给定输入值和期望的输出值,然后寻找两者之间的相关性。
Legendre的算法需要反复修改m和b并计算误差平方,非常耗时。
1909年,荷兰的Peter Debye简化了Legendre的方法。用Y表示X误差,Legendre的算法是找到使误差最小的X,在下图中,可以看到当X=1.1时,误差Y取到最小值。
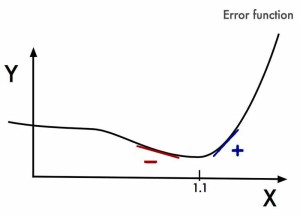
Debye注意到最低点左边的斜率是负的,而另一边则是正的。因此,如果知道了任意给定X的斜率值,就可以找到Y的最小值点。这就是梯度下降算法的基本思想,几乎所有的机器学习模型都会用到梯度下降算法。
假设误差函数为:
\[Error = x ^5 -2x^3-2 \]
这是一个极值问题,对其求导即可:
\[Error’ = 5 x ^4 - 6 x^2 \]
current_x = 0.5 # the algorithm starts at x=0.5
learning_rate = 0.01 # step size multiplier
num_iterations = 60 # the number of times to train the function
#the derivative of the error function (x**4 = the power of 4 or x^4)
def slope_at_given_x_value(x):
return 5 * x**4 - 6 * x**2
# Move X to the right or left depending on the slope of the error function
for i in range(num_iterations):
previous_x = current_x
current_x += -learning_rate * slope_at_given_x_value(previous_x)
print(previous_x)
print("The local minimum occurs at %f" % current_x)
通过向斜率相反方向去寻找x使误差逼近最低点,也就是在learning_rate前需要加一个负号。
最小二乘法配合梯度下降算法,就是线性回归过程。在20世纪50到60年代,一批实验经济学家在早期的计算机上实现了这些想法。
#Price of wheat/kg and the average price of bread
wheat_and_bread = [[0.5,5],[0.6,5.5],[0.8,6],[1.1,6.8],[1.4,7]]
def step_gradient(b_current, m_current, points, learningRate):
b_gradient = 0
m_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i][0]
y = points[i][1]
b_gradient += -(2/N) * (y - ((m_current * x) + b_current))
m_gradient += -(2/N) * x * (y - ((m_current * x) + b_current))
new_b = b_current - (learningRate * b_gradient)
new_m = m_current - (learningRate * m_gradient)
return [new_b, new_m]
def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
b = starting_b
m = starting_m
for i in range(num_iterations):
b, m = step_gradient(b, m, points, learning_rate)
return [b, m]
gradient_descent_runner(wheat_and_bread, 1, 1, 0.01, 100)
将梯度下降运用到误差函数上,是上述算法的的一个关键点。
[TOP]
1943年,心理学家Warren McCulloch和数学家Walter Pitts参考生物神经元的结构,发表了抽象的M-P神经元模型,并证明了单个神经元可以执行逻辑功能。
1957年,Frank Rosenblatt以M-P模型为基础,提出了感知器(perceptron)模型,并因此登上了《纽约时报》的头条(New Navy Device Learns By Doing)。
感知器模型沿用至今,下面是一个具有“或”逻辑功能的感知器。
from random import choice
from numpy import array, dot, random
result_or = lambda x: 0 if x < 0 else 1
training_data = [ (array([0,0,1]), 0),
(array([0,1,1]), 1),
(array([1,0,1]), 1),
(array([1,1,1]), 1), ]
weights = random.rand(3)
errors = []
learning_rate = 0.2
num_iterations = 100
for i in range(num_iterations):
input, truth = choice(training_data)
result = dot(weights, input)
error = truth - 1_or_0(result)
errors.append(error)
weights += learning_rate * error * input
for x, _ in training_data:
result = dot(x, weights)
print("{}: {} -> {}".format(input[:2], result, result_or(result)))
1969年,MIT AI实验室的Marvin Minsky和Seymour Papert指出感知器无法进行“异或”的运算,还批判了多层感知器构建神经网络模型的想法。尽管此后有人提出新的理论和模型,相关的研究均没有被主流重视,神经网络开始了长达十多年的低潮期。
1986年,D.E.Rumelhart等人在多层神经网络模型的基础上,提出了多层神经网络权值修正的反向传播学习算法——BP算法(Error Back-Propagation),解决了多层前向神经网络的学习问题,证明了多层神经网络具有很强的学习能力。
感知器由一组连接、一个求和单元和一个激活函数构成。感知器可以接收多个输入\((x_1, x_2, x_3, \cdots, x_n)\),每个输入上有一个权值\((\omega _1, \omega _2, \omega _3, \cdots, \omega _n)\),此外输入层还有一个偏置项\(\omega _0 = b\),相当于线性函数中的常数项。感知器的输出可记为:
\[y=f(\omega ^T \cdot x + b)\]
感知器需要有一个激活函数\(f(z)\),可以是sgn、sigmoid、TanH(双曲正切)等形式:
\[Sigmoid(z)=\frac{1}{1+e^{-z}}\]
\[TanH(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}\]
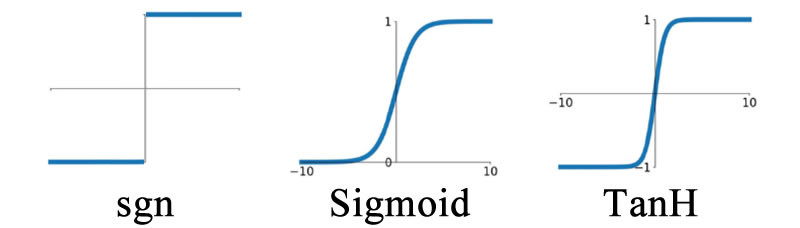
激活函数赋予感知器非线性映射能力。
机器学习所说的神经元和感知器实际上是一样的,习惯上,激活函数为阶跃函数(sgn)时称为感知器,而激活函数为sigmoid或tanh等连续函数时称为神经元。
多个神经元按照一定的规则连接起来,就构成了神经网络。
神经网络结构可被划分为层次型网络和互连型网络,层次型网络结构内只有相邻层的各节点之间存在连接,同层以及跨层的节点之间无连接。互连型网络结构中节点之间的连接无任何限制,任意两个节点都可以相连。
按照网络信息的流向,神经网络也可以划分为前馈型网络和反馈型网络,前馈型网络中前一层的输出作为下一层的输入,信息逐层传递,反馈型网络中所有节点不仅可以接受外界的输入信息,还能对外界输出信息。
神经网络由一个输入层、一个输出层和n个隐藏层构成,如将一个神经网络的输入记为向量\(x\),输出记为向量\(y\),第一个隐藏层的输出记为向量\(a_1\),从输入层到第一个隐藏层的权重记为矩阵\(W_1\),第二个隐藏层的输出记为向量\(a_2\),第一个隐藏层到第二个隐藏层的权重记为矩阵\(W_2\),第n个隐藏层的输出记为向量\(a_n\),从第n-1到第n个隐藏层的权重记为\(W_n\),则有
\[a_1=f(W_1 \cdot x)\]
\[a_2=f(W_2 \cdot a_1)\]
\[a_n=f(W_n \cdot a_{n-1})\]
\[y=f(W_{n+1} \cdot a_n)\]
这就是神经网络输出值的计算方法。
补充说明:某一层的输出向量维数与该层神经元个数相同,权重矩阵的维数为(上层神经元个数+1)*(本层神经元个数),这里的“+1”是因为隐藏层和输出层的神经元都会设置一个偏置项。
神经网络的训练就是确定权重矩阵的过程,非偏置节点连接上的值称为权重(weight),而偏置节点上的值称为偏置,两者统称为参数(parameter);而神经网络的连接方式、网络的层数、每层的节点数则需要人为预先设置,称为超参数。
已知一组\(x\)和\(y\),确定系数\(\omega\),记\(e=x \omega -y\),采用梯度下降算法,\(\omega\)的迭代式为:
\[\omega:=\omega+ \eta x^T e\]
\(\eta\)是步长,也被称为学习速率。当达到指定迭代次数或迭代误差时,即可确定\(\omega\),完成神经元的训练,此时输入一个新的\(x\),神经元给出一个\(y\)的预测值。
如果神经元的激活函数为sigmoid函数,首先可以计算该神经网络输出层节点\(i\)的误差为:
\[ \delta _i = y_i(1-y_i)(\hat y _i-y_i) \]
其中,\(\hat y _i\)是节点\(i\)的目标值,\(y_i\)是节点\(i\)的输出值。
得到输出层误差项后,可逐层计算隐藏层节点\(i\)的误差:
\[ \delta _i = a_i(1-a_i)\Sigma \omega _{ki}\delta _k \]
\(a_i\)是节点\(i\)的输出值,\(\omega _{ki}\)是节点\(i\)到其下一层节点\(k\)的连接权值,\(\delta _k\)是节点\(i\)的下一层节点\(k\)的误差项。
最后,更新每个连接上的权值:
\[ \omega _{ji} := \omega _{ji} + \eta \delta _j x _{ji} \]
其中,\( \omega _{ji} \)是节点\(i\)到节点\(j\)的权重,\(\eta\)是学习速率,\(\delta _j\)是节点\(j\)的误差项,\( x _{ji} \)是节点\(i\)传递给节点\(j\)的输入。该公式中的\( \delta _j x _{ji} \)就是算法计算出的梯度。
可以看到,计算一个节点的误差需要先计算与之相连的下一层节点的误差,对于整个神经网络来说,需要首先计算输出层的误差,然后反向依次计算每个隐藏层的误差,直到与输入层相连的那个隐藏层,这就是“反向传播算法”的含义。所有节点的误差项计算完毕,就可以更新所有连接的权重了。
关于反向传播算法的推导,可查看这里。
我们来看看反向传播是如何解决“异或”运算的。
import numpy as np
X_XOR = np.array([[0,0,1], [0,1,1], [1,0,1],[1,1,1]])
y_truth = np.array([[0],[1],[1],[0]])
np.random.seed(1)
syn_0 = 2*np.random.random((3,4)) - 1
syn_1 = 2*np.random.random((4,1)) - 1
def sigmoid(x):
output = 1/(1+np.exp(-x))
return output
def sigmoid_output_to_derivative(output):
return output*(1-output)
for j in range(60000):
layer_1 = sigmoid(np.dot(X_XOR, syn_0))
layer_2 = sigmoid(np.dot(layer_1, syn_1))
error = layer_2 - y_truth
layer_2_delta = error * sigmoid_output_to_derivative(layer_2)
layer_1_error = layer_2_delta.dot(syn_1.T)
layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)
syn_1 -= layer_1.T.dot(layer_2_delta)
syn_0 -= X_XOR.T.dot(layer_1_delta)
print("Output After Training: \n", layer_2)
该模型同时使用了反向传播、矩阵乘法、梯度下降,解决了神经网络的“异或”问题,神经网络又被重新重视起来,一时间,上百种神经网络模型被提出来。训练神经网络需要的计算量很大,局部最优解的存在和隐藏层节点超参数进一步增加了训练难度。同时期发展起来的支持向量机,计算量相对较低,并且很容易获得全局最优解,也没有超参数,在工程应用上迅速超越神经网络。90年代中期,神经网络的研究再次进入低潮期。
现在,让我们稍微停顿一下,来看看神经网络如何处理回归和分类问题。
首先加载相关模块:
from keras.models import Sequential
from keras.layers import Dense
import matplotlib as plt
Sequential用于逐层建立神经网络,可以一层一层地添加,Dense表示该神经层为全连接层。
训练集的可视化:
plt.scatter(X,y)
plt.show()
建立神经网络:
model_r = Sequential()
model_r.add(Dense(units=1,input_dim=1))
model_r.add是添加层,此处添加了Dense全连接层,输入和输出数据的维度都是1。
指定损失函数和优化方法并编译:
model_r.compile('sgd','mse')
optimizer和loss是compile必要的两个参数。keras源码中compile的定义是这样的:
compile(self, optimizer, loss, metrics=None, sample_weight_mode=None)
optimizer: 字符串,指定优化器。下文将会详细讨论优化器的种类、作用和选择方法。
loss: 字符串,损失函数,包括mse,mae,mape,msle,kld,cosine等,关于损失函数的概念,可参考这里,常用的损失函数,可参考这里。
metrics: 列表,模型的评估指标,典型用法是metrics=['accuracy']。
sample_weight_mode: 样本权重,默认为None,可选temporal,表示按时间步为样本赋权(2D权矩阵)。
开始训练:
model_r.train_on_batch(X_train,y_train)
模型评估:
model_r.evaluate(X_test,y_test,batch_size=40)
模型参数:
model_r.layers[0].get_weights()
返回权值和偏置项。
回归曲线:
y_pred = model_r.predict(X_test)
plt.scatter(X_test,y_test)
plt.plot(X_test,y_pred)
plt.show()
建立,编译,训练,评估是使用keras解决问题的四个基本步骤。
可以将训练好的模型保存起来:
model_r.save('nn.h5')
读取该模型时,需要使用load_model:
from keras.models import load_model
model_r = load_model('nn.h5')
加载相关模块:
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import RMSprop
建立神经网络:
model_c = Sequential([Dense(32,input_dim=784),Activation('relu'),Dense(10),Activation('softmax'),])
建立网络时直接添加层,其中第一层有32个输出维度,784个输入维度,激活函数为relu,第二层接收上一层输入的32个维度,输出10个维度给softmax。
定义优化器,可以加速训练:
rmsprop = RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0)
指定损失函数、优化方法和评估参数并编译:
model_c.compile(optimizer=rmsprop,loss='categorical_crossentropy',metrics=['accuracy'])
训练模型:
model_c.fit(X_train,y_train,epochs=2,batch_size=32)
模型评估:
model_c.evaluate(X_test,y_test)
将给出误差和准确度。
[TOP]
从90年代中期,神经网络再次进入低潮期,但仍有几位学者试图寻找突破点,2006年,加拿大多伦多大学的Geoffery Hinton教授正式提出了“深度学习”的概念,引入了“预训练”(pre-training),使神经网络快速找到一个接近最优解的权重矩阵,之后再对其进行“微调”(fine-tuning),这种方法大幅度减少了训练时间。
深层网络的表达力更强。一个仅有一个隐藏层的神经网络就能拟合任何一个函数,但是它需要很多神经元。而深层网络用较少的神经元就能拟合同样的函数。也就是为了拟合一个函数,要么使用一个浅而宽的网络,要么使用一个深而窄的网络,深而窄的网络往往更节约资源。
训练深层网络需要大量数据,同时还需要很多技巧,这是因为深度学习仍然在快速发展中,各种算法的系统性仍有待归纳,最新的成果可查看这些论文。
2012年,卷积神经网络(Convolutional Neural Network, CNN)在图像识别领域的突出表现,正式引爆了深度学习的研究。神经网络模型的层数逐年增加,各种优化方法层出不穷。
感知器使用的激活函数是sgn函数,两层神经网络使用的最多的是sigmoid函数,深度网络则使用更容易使结果收敛的ReLU(Rectified Linear Unit, 修正线性单元)函数。
机器学习中的激活函数(active function)有时候也称为转移函数(transfer function)。
ReLU函数的表达式为:
\[ReLU(z)=max(0,z)\]
ReLU函数有很多优势,如sigmoid函数需要计算指数和倒数,而ReLU函数则不需要,计算量大幅减小;sigmoid导数最大值为1/4,反向传播算法计算梯度时,每经过一层sigmoid神经元,梯度就要乘上一次sigmoid导数,梯度就会越来越小,对于深度网络就会发生所谓梯度消失的现象,而ReLU导数为1,不会引起梯度变小,因此,使用ReLU激活函数可以训练更深的网络;采用sigmoid激活函数的神经网络,约有50%的神经元会被激活,而ReLU函数在输入小于0时是完全不激活的,因此神经元的激活率更低,节省了计算资源。ReLU有一个缺陷,就是它在负区间的导数为0,可能导致某一个节点永远不参与模型的学习过程。
Google Brain于最近(2017.10)提出了一种新的激活函数:
\[Swish(z)= y = z \cdot sigmoid(z)\]
其导数为:
\[Swish’(z) = y +sigmoid(z)(1-y)\]
该函数有效缓解了梯度消失,比ReLU更适于处理深度学习问题。
假如有\(a\),\(b\)两个数,如果\(a>b\),则\(max(a,b)\)会直接取\(a\),有时候,我们希望依据概率从\(a\),\(b\)中取值,softmax就是这样一种函数:
\[softmax(z) _i = \frac{e ^{z _i}}{ \Sigma _{k=1} ^{K} e ^{z _{k}}} \]
这样就可以实现\(K\)元分类,上式表示将\(z\)分到类别\(i\)的概率。softmax常用于网络的最后一层节点。
这里的“优化”是指对梯度下降算法和反向传播算法的优化,keras预定义了sgd, rmsprop, adagrad, adadelta, adam, adamax, nadam等优化器,可查看这里。
如果数据是稀疏的,就选用Adagrad, Adadelta, RMSprop, Adam,尤其是Adam,在RMSprop的基础上加了bias-correction和momentum,几乎是目前最好用的优化器。
损失函数(loss function)也被称为代价函数(cost function)或目标函数(objective function),简单地说就是真实值和预测值的误差平方和(mse):
\[ f(\omega) = \frac{1}{2}(X \omega -y)^T(X \omega -y) \]
其中X为特征矩阵,y是标签向量,\(\omega\)是回归系数。
除了mse,keras预定义的损失函数还有mae,mape,msle等等,其含义可参考这里。
为了限制模型的复杂度,抑制过拟合,提高泛化能力,需要对损失函数进行调整和修正,这种处理方法被称为“正则化”(regularization,翻译为正则并不恰当,不如直接称之为调整或修正),如引入L2惩罚项:
\[ E(\omega) = \frac{1}{2}(X \omega -y)^T(X \omega -y) + \frac{1}{2} \lambda \omega ^T \omega \]
\(E(\omega)\)称为误差函数(error function),\(\lambda\)称为正则化系数,\(\lambda\)越大,正则越强。
除了引入惩罚项,还有一些其它的正则化技术,如:
Dropout 在神经网络训练时保持输入和输出层不变,每次迭代过程中“随机”临时删除隐藏层的一部分神经元。采用Dropout的训练过程,相当于训练了很多个只有半数隐藏层神经元的神经网络(“半数网络”),每一个半数网络都可以给出一个分类结果,这些结果有的是正确的,有的是错误的,随着训练的进行,大部分半数网络都可以给出正确的分类结果,那么少数错误分类结果就不会对最终结果造成大的影响。
Data Augmentation 即数据扩容,这并不是要真正去重新收集数据以扩充数据集,而是对已有的数据集进行处理,如将图片旋转一个小角度、添加随机噪声、截取图片的一部分等等,增加训练量,从而获得更好的结果。
[TOP]
卷积神经网络(CNN, Convolutional Neural Network)是目前神经网络领域的一个热点,主要用于图像、语音识别,Google的GoogleNet、AlphaGo、微软的ResNet等都用到了CNN算法。
练习数据集:
CIFAR是由加拿大先进技术研究院的AlexKrizhevsky, Vinod Nair和Geoffrey Hinton收集的小图片数据集,包含CIFAR-10和CIFAR-100两个数据集。 CIFAR-10由60000张32*32的RGB彩色图片构成,共10个分类。50000张训练,10000张测试(交叉验证)。这个数据集最大的特点在于将识别迁移到了普适物体,而且应用于多分类。CIFAR-100由60000张图像构成,包含100个类别,每个类别600张图像,其中500张用于训练,100张用于测试。其中这100个类别又组成了20个大的类别,每个图像包含小类别和大类别两个标签。官网提供了Matlab,C,python三个版本的数据格式。
全连接神经网络在处理图像时不可避免地遇到了以下几个问题:
参数数量太多 考虑一个输入1000*1000像素的图片(一百万像素,现在已经不能算大图了),输入层有1000*1000=100万节点。假设第一个隐藏层有100个节点(这个数量并不多),那么仅这一层就有(1000*1000+1)*100=1亿参数,这实在是太多了!我们看到图像只扩大一点,参数数量就会多很多,因此它的扩展性很差。
没有利用像素之间的位置信息 对于图像识别任务来说,每个像素和其周围像素的联系是比较紧密的,和离得很远的像素的联系可能就很小了。如果一个神经元和上一层所有神经元相连,那么就相当于对于一个像素来说,把图像的所有像素都等同看待,这不符合前面的假设。当我们完成每个连接权重的学习之后,最终可能会发现,有大量的权重,它们的值都是很小的(也就是这些连接其实无关紧要)。努力学习大量并不重要的权重,这样的学习必将是非常低效的。
网络层数限制 我们知道网络层数越多其表达能力越强,但是通过梯度下降方法训练深度全连接神经网络很困难,因为全连接神经网络的梯度很难传递超过3层。因此,我们不可能得到一个很深的全连接神经网络,也就限制了它的能力。
解决这些问题的思路有:
局部连接 每个神经元不再和上一层的所有神经元相连,而只和一小部分神经元相连,这样可以减少很多参数。
权值共享 一组连接可以共享同一个权重,而不是每个连接有一个不同的权重,这样又减少了很多参数。
下采样 使用池化层来减少每层的样本数,进一步减少参数数量,同时还可以提升模型的鲁棒性(Robust,健壮,表征在异常和危险情况下系统的生存能力)。
CNN就是从这些思路出发,尽可能保留重要参数,去掉大量不重要的参数,达到了更好的学习效果。
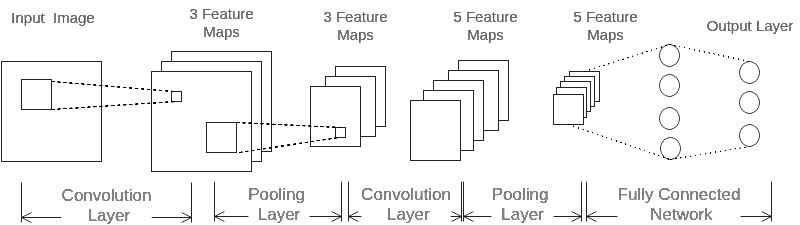
如图所示,CNN由输入层(INPUT)、卷积层(CONV)、池化层(POOL, Pooling)、全连接层(FC)、输出层(OUTPUT)组成,即INPUT-[CONV*1-POOL]*2-FC*2-OUTPUT。
CNN每层的神经元都是三维排列的,有长度、宽度和厚度,卷积就是将长宽减小、厚度增加的过程。
对于上图展示的神经网络,我们看到输入层的长度和宽度对应于输入图像的长度和宽度,而它的厚度为1。接着,第一个卷积层对这幅图像进行了卷积操作,得到了三个Feature Map。这里的”3”可能是让很多初学者迷惑的地方,实际上,就是这个卷积层包含三个Filter,也就是三套参数,每个Filter都可以把原始输入图像卷积得到一个Feature Map,三个Filter就可以得到三个Feature Map。至于一个卷积层可以有多少个Filter,那是可以自由设定的。也就是说,卷积层的Filter个数也是一个超参数。我们可以把Feature Map可以看做是通过卷积变换提取到的图像特征,三个Filter就对原始图像提取出三组不同的特征,也就是得到了三个Feature Map,也称做三个通道(channel)。
继续观察,在第一个卷积层之后,池化层对三个Feature Map做了下采样,得到了三个更小的Feature Map。接着,是第二个卷积层,它有5个Filter。每个Fitler都把前面下采样之后的3个Feature Map卷积在一起,得到一个新的Feature Map。这样,5个Filter就得到了5个Feature Map。接着,是第二个Pooling,继续对5个Feature Map进行下采样,得到了5个更小的Feature Map。
上图所示网络的最后两层是全连接层。第一个全连接层的每个神经元,和上一层5个Feature Map中的每个神经元相连,第二个全连接层(也就是输出层)的每个神经元,则和第一个全连接层的每个神经元相连,这样得到了整个网络的输出。
如图所示,有一个5*5的图像,使用一个3*3的filter进行卷积,步幅(stride)为1。
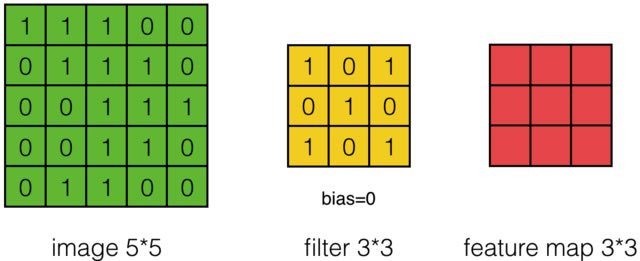
首先对图像的每个像素进行编号,用\(x _{i,j}\)表示图像的第\(i\)行第\(j\)列元素;对filter的每个权重进行编号,用\( \omega _{m,n}\)表示第行\(m\)第\(n\)列权重,用\( \omega _b\)表示filter的偏置项;对Feature Map的每个元素进行编号,用\(a _{i,j}\)表示Feature Map的第\(i\)行第\(j\)列元素;用\(f\)表示激活函数(如ReLU函数)。上图可使用下列公式计算卷积:
\[ a _{i,j} = f(\Sigma ^2 _{m=0} \Sigma ^2 _{n=0} \omega _{m,n} x _{i+m,j+n} + \omega _b) \]
计算过程和结果如下图:
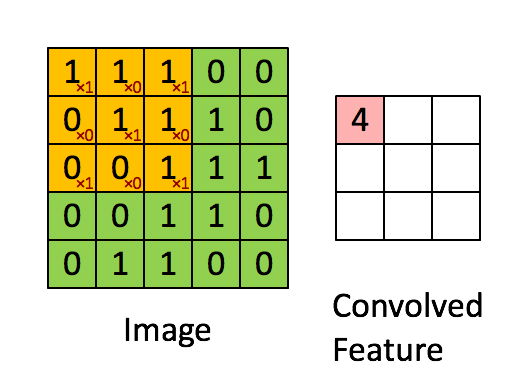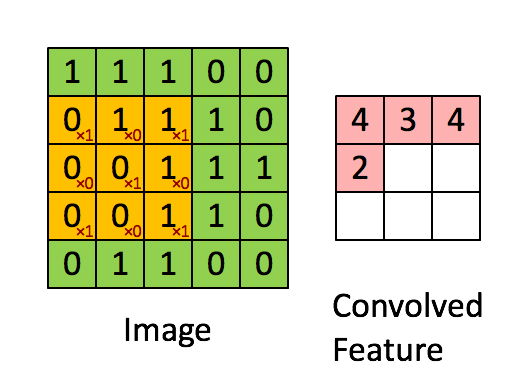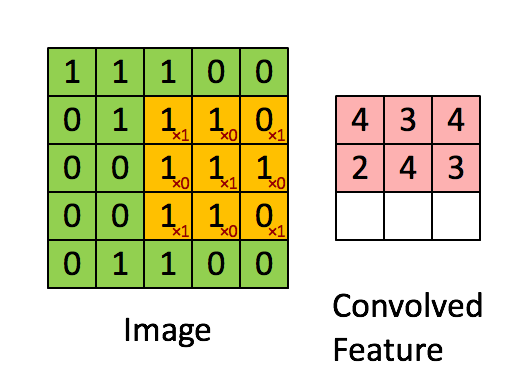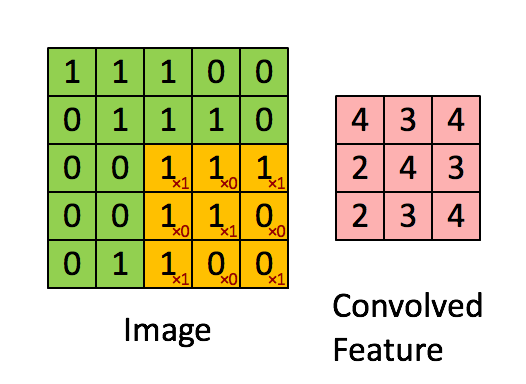
如果步幅为2,则结果为:
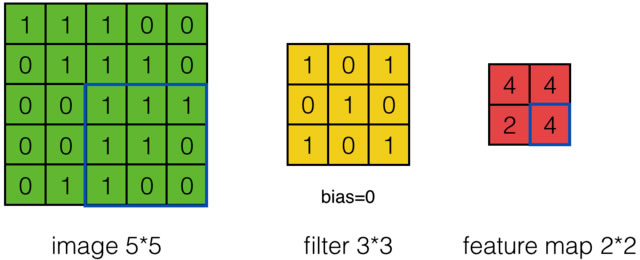
图像边长\(W _1\),步幅\(S\),filter边长\(F\)和卷积后Feature Map的边长\(W _2\)有如下关系:
\[ W _2 = (W _1 - F + 2 P)/S +1 \]
上式中的\(P\)是Zero Padding数值,Zero Padding是指在原始图像周围补几圈0,这种处理方式有助于图像边缘部分的特征提取。
上面的初始图像深度(厚度)为1,如果图像深度为\(D\),则相应的filter的深度也必须是\(D\),此时卷积层输出的计算公式为:
\[ a _{d,i,j} = f(\Sigma ^{D-1} _{d=0} \Sigma ^{F-1} _{m=0} \Sigma ^{F-1} _{n=0} \omega _{d,m,n} x _{d,i+m,j+n} + \omega _b) \]
每个卷积层可以有多个filter,每个filter和原始图像进行卷积后,都可以得到一个Feature Map,因此,卷积后Feature Map的深度和卷积层的filter个数是相同的。
下图是7*7*3图像,经过两个3*3*3filter的卷积(步幅为2)过程,得到3*3*2的输出,其中Zero Padding为1,即在输入元素的周围补了一圈0。
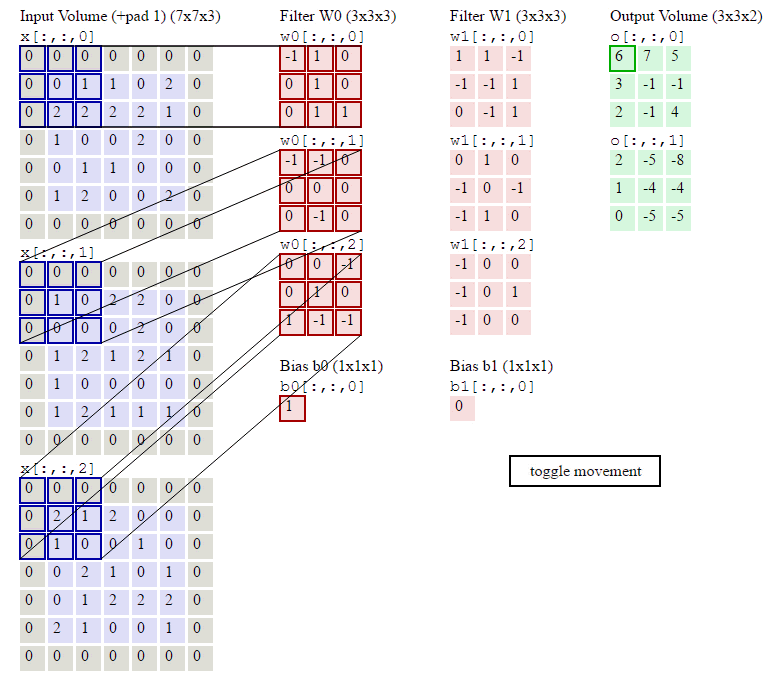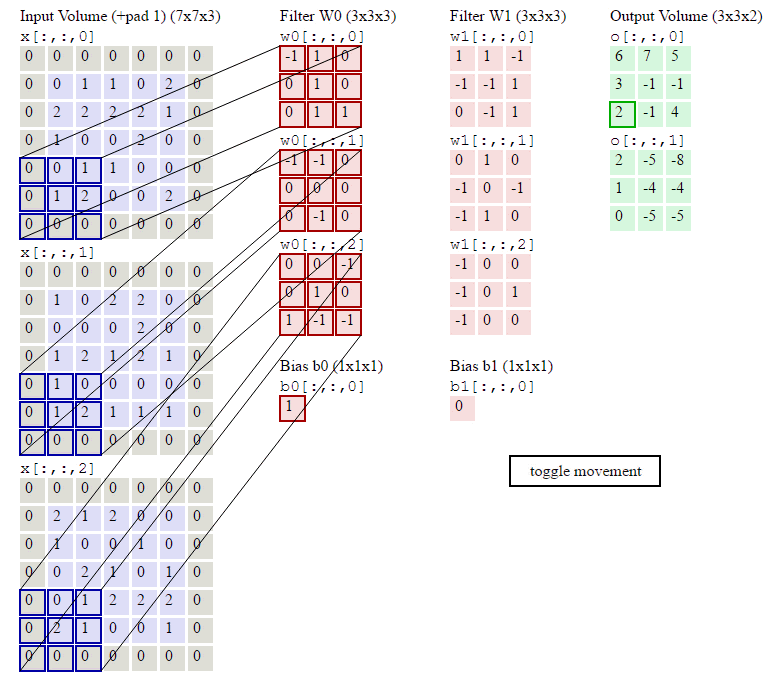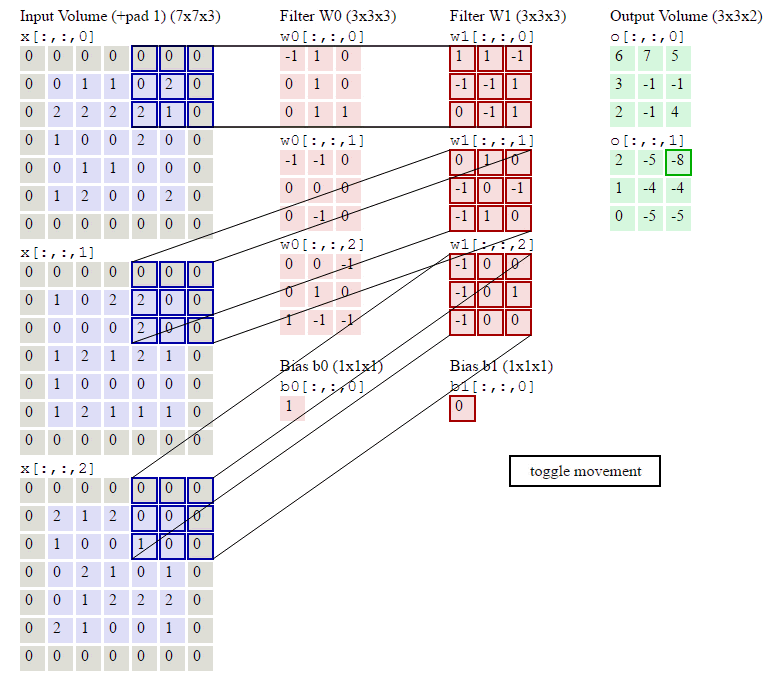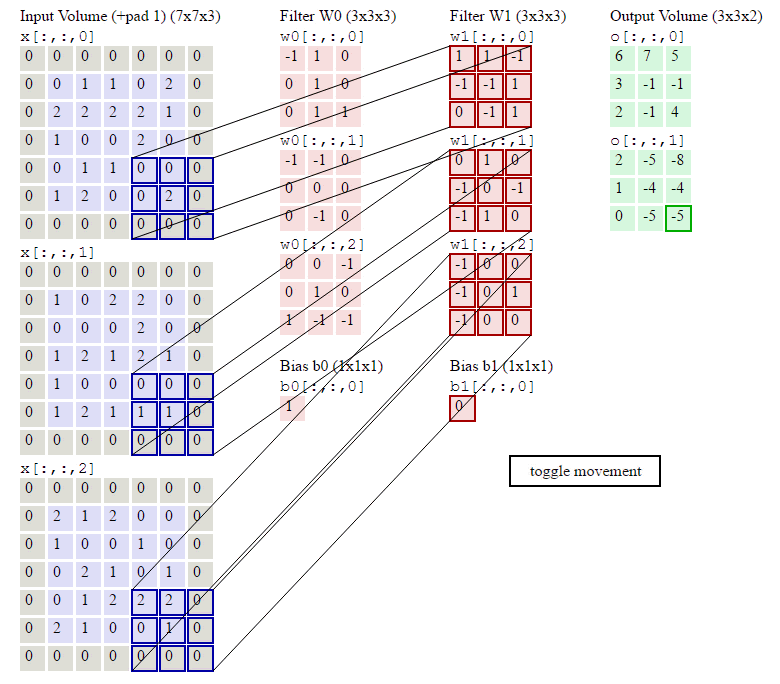
可以看到,与全连接神经网络相比,CNN通过局部连接和权值共享,使参数数量大大减少了。
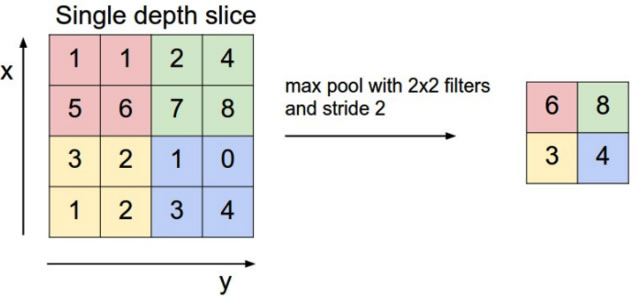
池化层主要的作用是下采样,通过去掉Feature Map中不重要的样本,进一步减少参数数量。Pooling的方法很多,最常用的是Max Pooling。Max Pooling实际上就是在n*n的样本中取最大值,作为采样后的样本值,如下图。除了Max Pooing之外,常用的还有Mean Pooling(取池化窗口中各样本的平均值)和Stoastic Pooling(随机选择池化窗口中的一个样本值)。
对于深度为\(D\)的Feature Map,各层独立做Pooling,因此Pooling后的深度仍然为\(D\)。
CNN的训练采用反向传播算法,首先将误差项从输出层逐层上传,然后计算每个参数的梯度,最后更新参数,详细的推导过程可查看这里。
加载相关模块:
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation, Convolution2D, MaxPooling2D, Flatten
from keras.optimizers import Adam
建立CNN模型:
cnn_c = Sequential()
添加卷积层,输出为(32,28,28):
cnn_c.add(Convolution2D(batch_input_shape=(None,1,28,28),filter=32,kernel_size=5,strides=1,padding='same',data_format='channels_first',))
cnn_c.add(Activation('relu'))
添加池化层,max pooling,输出为(32,14,14):
cnn_c.add(MaxPooling2D(pool_size=2,strides=2,padding='same',data_format='channels_first',))
添加第二个卷积层,输出为(64,14,14):
cnn_c.add(Convolution2D(64,5,strides=1,padding='same',data_format='channels_first'))
cnn_c.add(Activation('relu'))
添加池化层,max pooling,输出为(64,7,7):
cnn_c.add(MaxPooling2D(2,2,'same',data_format='channels_first'))
添加全连接层,输入为(64,7,7),输出为1024维向量:
cnn_c.add(Flatten())
cnn_c.add(Dense(1024))
cnn_c.add(Activation('relu'))
添加全连接层,输出为10维向量:
cnn_c.add(Dense(10))
cnn_c.add(Activation('softmax'))
定义优化器:
adam = Adam(lr=1e-4)
指定优化方法、损失函数和评估参数并编译:
cnn_c.compile(optimizer=adam,loss='categorical_crossentropy',metrics=['accuracy'])
训练模型:
cnn_c.fit(X_train,y_train,epochs=1,batch_size=64,)
模型评估:
cnn_c.evaluate(X_test, y_test)
将给出误差和准确度。
[TOP]
卷积神经网络处理的数据集,前一个输入和后一个输入是相互独立的,而现实中经常需要处理某些“序列”,前面的输入和后面的输入是有关联的,如一个句子,词和词之间构成一个序列,或者一段视频,帧和帧之间构成一个序列,这就用到了另一类重要的神经网络:循环神经网络(RNN, Recurrent Neural Network)。
RNN最先被用于自然语言处理,比如语言模型就可以使用____来构建。
给定一句话的一部分,如上面这句话,语言模型可以预测缺失的部分最可能的一个词是什么,也就是说,语言模型可以“完形填空”。
在RNN出现之前,语言模型主要采用N-Gram,N是一个自然数,表示一个词出现的概率只与前面N个词相关。对上面这句话分词:
RNN 最先 被 用于 自然 语言 处理 , 比如 语言 模型 就 可以 使用 __ 来 构建。
2-Gram模型在填空时,只能看到前面的“使用”,3-Gram可以看到“可以使用”,显然都无法准确完成填空,因为这句话的关键信息“RNN”远在14个词之前。可见N-Gram模型在处理任意长度的句子时并不合适,而且,随着N的增大,模型的复杂度指数级提高,需要占用海量内存。
RNN就为此而生,RNN可以向前或向后看到任意多个词。
下图是一个简单的RNN,由输入层、输出层和一个隐藏层组成:
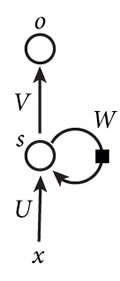
\(x\)是输入层的值,\(o\)是输出层的值,\(s\)是隐藏层的值,U是输入层到隐藏层的权重矩阵,V是隐藏层到输出层的权重矩阵,W是隐藏层上一次的值作为这一次的输入的权重矩阵,将该网络在时间维度上展开就得到:
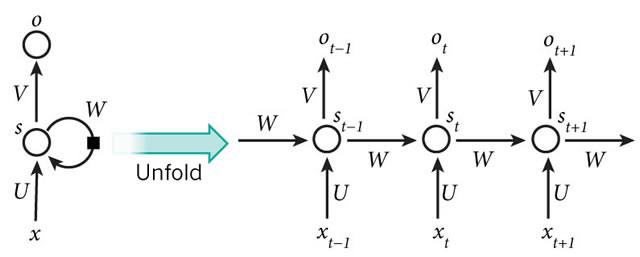
上面这个网络在\(t\)时刻接收到输入\(x _t\)之后,隐藏层的值是\(s _t\),输出值是\(o _t\),需要指出,\(s _t\)不仅与\(x _t\)有关,还与\(s _{t-1}\)有关,其计算方法为:
\[o _t = g(V s _t) \]
\[s _t = f(U x _t + W s _{t-1}) \]
\(g\)和\(f\)是激活函数。可以看到\(o _t\)与\(x _t\)、\(x _{t-1}\)、\(x _{t-2}\)、\(x _{t-3}\)、…都有关系,这就是RNN可以向前看任意多输入值的原理。
只向前看还是不够的,还需要向后看,于是,双向循环神经网络出现了:
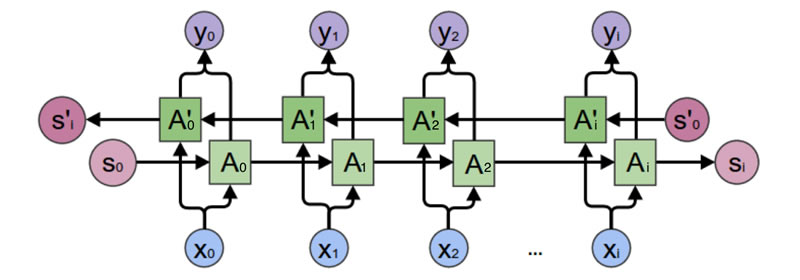
时间正向和反向的输出值需要分别计算,再将结果加和:
\[o _t = g(V s _t + V’ s’ _t) \]
\[s _t = f(U x _t + W s _{t-1}) \]
\[s’ _t = f(U’ x _t + W’ s’ _{t-1}) \]
正向计算和反向计算不共享权重,U、V、W和U’、V’、W’都是不同的权重矩阵。
对于深度循环神经网络:
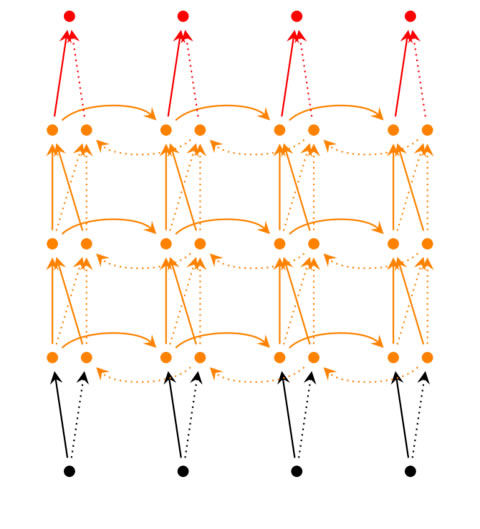
若第\(i\)个隐藏层的值表示为\(s ^{(i)} _t\)、\(s’ ^{(i)} _t\),则深度循环神经网络的计算公式为:
\[o _t = g(V ^{(i)} s ^{(i)} _t + V’ ^{(i)} s’ ^{(i)} _t) \]
\[s ^{(i)} _t = f(U ^{(i)} s ^{(i-1)} _t + W ^{(i)} s _{t-1}) \]
\[s’ ^{(i)} _t = f(U’ ^{(i)} s’ ^{(i-1)} _t + W’ ^{(i)} s’ _{t-1}) \]
…
\[s ^{(1)} _t = f(U ^{(1)} x _t + W ^{(1)} s _{t-1}) \]
\[s’ ^{(1)} _t = f(U’ ^{(1)} x _t + W’ ^{(1)} s’ _{t-1}) \]
与反向传播算法(BP)类似,循环神经网络采用BPTT(Backpropagation Through Time)算法,首先计算每个神经元的输出值,反向计算每个神经元的误差项(误差函数对加权输入的偏导数),再计算每个权重的梯度,最后用梯度下降算法更新权重。
记神经元在\(t\)时刻的加权输入为\(net _t\),即:
\[net _t = U x _t + W s _{t-1}\]
记根据向量\(a\)创建的对角矩阵为\(diag(a)\),即:
\[ diag(a) = \begin{pmatrix}
a _1 & 0 & … 0\\
0 & a _2 & … 0\\
…\\
0 & 0 & … a _n
\end{pmatrix} \]
则在任意时刻\(k\)的误差项\(\sigma _k\)为:
\[\sigma ^T _k = \sigma ^T _t \prod ^ {t-1} _{i=k} W diag [f’(net _i)]\]
这就是将误差项沿时间反向传播的算法。将误差项由\(l\)层反向传递到上一层\((l-1)\)的公式为:
\[(\sigma ^{l-1} _t )^T = (\sigma ^l _t)^T U diag[f’ ^{l-1} (net ^{l-1} _t)]\]
分析误差项\(\sigma _k\)可以发现:
\[\vert \vert \sigma ^T _k \vert \vert \leqslant \vert \vert \sigma ^T _t \vert \vert \prod ^{t-1} _{i=k} \vert \vert W \vert \vert \vert \vert diag [f’ (net _i)] \vert \vert\]
\[ \leqslant \vert \vert \sigma ^T _t \vert \vert (\beta _W \beta _f) ^{t-k}\]
式中\(\beta\)定义为矩阵的模的上界。当指数\((t-k)\)很大时候(即向前看很远的时候),会引起误差项的值增长或缩小非常快,从而导致梯度爆炸或梯度消失。长短时记忆网络(LSTM, Long Short Term Memory)就是为了解决这个问题而构建的。
RNN不只是可以处理语言、视频这样的序列问题,对于与时间无关的问题,也可以按照序列化的方式去处理。
加载相关模块:
import numpy as np
from keras.models import Sequential
from keras.layers import SimpleRNN, Activation, Dense
from keras.optimizers import Adam
初始化参数:
TIME_STEPS = 28 # same as the height of the image
INPUT_SIZE = 28 # same as the width of the image
BATCH_SIZE = 50
BATCH_INDEX = 0
OUTPUT_SIZE = 10
CELL_SIZE = 50
LR = 0.001
建立模型:
rnn = Sequential()
添加SimpleRNN:
rnn.add(SimpleRNN(batch_input_shape=(None, TIME_STEPS, INPUT_SIZE),output_dim=CELL_SIZE,unroll=True))
添加Dense输出层:
rnn.add(Dense(OUTPUT_SIZE))
rnn.add(Activation('softmax'))
定义优化器:
adam = Adam(LR)
编译:
rnn.compile(optimizer=adam,loss='categorical_crossentropy',metrics=['accuracy'])
训练:
for step in range(4001):
X_batch = X_train[BATCH_INDEX: BATCH_INDEX+BATCH_SIZE, :, :]
Y_batch = y_train[BATCH_INDEX: BATCH_INDEX+BATCH_SIZE, :]
cost = model.train_on_batch(X_batch, Y_batch)
BATCH_INDEX += BATCH_SIZE
BATCH_INDEX = 0 if BATCH_INDEX >= X_train.shape[0] else BATCH_INDEX
if step % 500 == 0:
cost, accuracy = model.evaluate(X_test, y_test, batch_size=y_test.shape[0], verbose=False)
print('test cost: ', cost, 'test accuracy: ', accuracy)
[TOP]
由于梯度爆炸和梯度消失,循环神经网络难以处理长距离的依赖,长短时记忆网络(LSTM),则成功解决了这一缺陷。
LSTM引入一个单元状态(cell state),用来保存长期记忆。
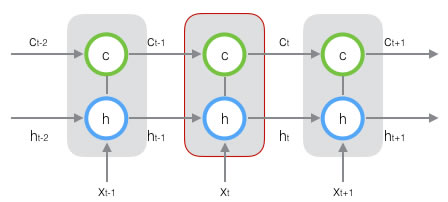
可以看到,在\(t\)时刻,LSTM有三个输入:当前时刻网络的输入值\(x _t\),上一时刻LSTM的输出值\(h _{h-1}\),上一时刻的单元状态\(c _{t-1}\);两个输出:当前时刻LSTM输出值\(h _t\),当前时刻的单元状态\(c _t\)。
为了控制状态\(c\),LSTM用两个门来控制单元状态\(c\)的内容,一个是遗忘门(forget gate),用来决定上一个时刻的单元状态\(c _{t-1}\)有多少保留到当前时刻\(c _t\),另一个是输入门(input gate),用来决定当前时刻网络的输入\(x _t\)有多少保存到单元状态\(c _t\);用输出门(output gate)来控制单元状态\(c _t\)有多少输出到LSTM的当前输出值\(h _t\),如图所示:
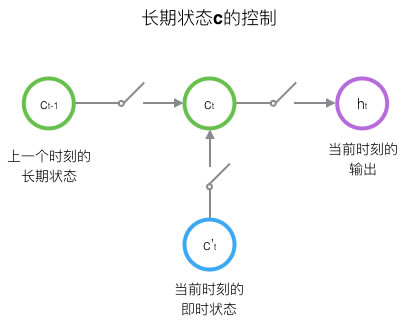
下图是LSTM一个节点的结构图:
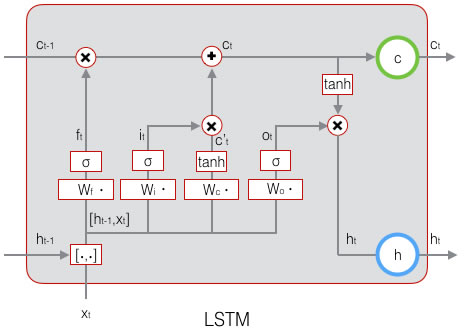
遗忘门的输出为:
\[f _t = \sigma (W _f \cdot [h _{h-1} , x _t] + b _f)\]
\(W _f\)是遗忘门的权重矩阵,\([h _{h-1} , x _t]\)表示把这两个向量连接成一个更长的向量,\(b _f \)是遗忘门的偏置项,\(\sigma\)是激活函数。
如果输入的维度为\(d _x\),隐藏层的维度为\(d _h\),单元状态的维度为\(d _x\),通常\(d _c = d _h\),则遗忘门的权重矩阵\(W _f\)维度是\(d _c \times (d _h + d _x)\)。\(W _f\)由两个矩阵拼接而成:
\[ [W _f] \begin{pmatrix}
h _{h-1}\\
x _t
\end{pmatrix} =
\begin{pmatrix}
W _{fh} & W _{fx}
\end{pmatrix}
\begin{pmatrix}
h _{h-1}\\
x _t
\end{pmatrix}
\]
\[ W _{fh} h _{h-1} + W _{fx} x _t\]
\(W _{fh}\)对应输入项\(h _{t-1}\),\(W _{fx}\)对应输入项\(x _t\)。
输入门为:
\[i _t = \sigma (W _i \cdot [h _{h-1} , x _t] + b _i)\]
\(W _i\)是输入门的权重矩阵,\(b _i\)是输入门的偏置项。
当前输入的单元状态为:
\[ \tilde{c _t} = tanh(W _c \cdot [h _{t-1} , x _t] + b _c)\]
当前时刻的单元状态为:
\[ c _t = f _t \circ c _{t-1} + i _t \circ \tilde(c _t) \]
\(\circ\)表示按元素乘,即numpy中的’broadcast’。
可以看到\(c _t\)可以保存很久之前的信息,也可以避免当前无关紧要的内容进入记忆。
输出门的输出为:
\[o _t = \sigma (W _o \cdot [h _{h-1} , x _t] + b _o) \]
LSTM的输出由输出门和单元状态共同确定:
\[h _t = o _t \circ tanh(c _t) \]
到此为止,已经完成LSTM前向计算每个神经元的的\(f _t\)、\(i _t\)、\(c _t\)、\(o _t\)、\(h _t\)五个向量的计算,通过反向传播算法,可以更新8组参数:
遗忘门的权重矩阵\(W _f\)和偏置项\(b _f\);
输入门的权重矩阵\(W _i\)和偏置项\(b _i\);
输出门的权重矩阵\(W _o\)和偏置项\(b _o\);
计算单元状态的权重矩阵\(W _c\)和偏置项\(b _c\)。
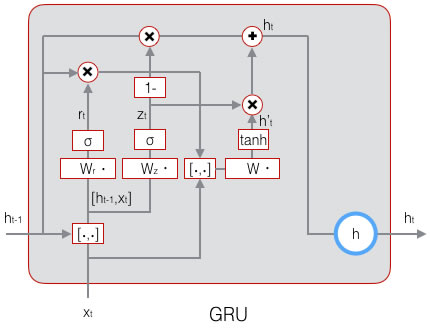
LSTM存在相当多的变体,其中GRU(Gated Recurrent Unit)简化了LSTM,仍保持着LSTM的效果,是当前最流行的RNN。
GRU将输入门、遗忘门、输出门变为更新门(update gate)\(z _t\)和重置门(reset gate)\(r _t\),同时将单元状态和输出合并为一个状态\(h\),其前向计算公式为:
\[z _t = \sigma (W _z \cdot [h _{t-1} , x _t])\]
\[r _t = \sigma (W _r \cdot [h _{t-1} , x _t])\]
\[ \tilde{h _t} = tanh(W \cdot [r _t \circ h _{t-1} , x _t] )\]
\[ h = (1 - z _t) \circ h _{h-1} + z _t \circ \tilde(h _t)\]
加载相关模块:
import numpy as np
from keras.models import Sequential
from keras.layers import LSTM, TimeDistributed, Dense
from keras.optimizers import Adam
初始化参数:
BATCH_START = 0
TIME_STEPS = 20
BATCH_SIZE = 50
INPUT_SIZE = 1
OUTPUT_SIZE = 1
CELL_SIZE = 20
LR = 0.006
定义一个get_batch函数:
def get_batch():
global BATCH_START, TIME_STEPS
xs = np.arange(BATCH_START, BATCH_START+TIME_STEPS*BATCH_SIZE).reshape((BATCH_SIZE, TIME_STEPS)) / (10*np.pi)
seq = np.sin(xs)
res = np.cos(xs)
BATCH_START += TIME_STEPS
return [seq[:, :, np.newaxis], res[:, :, np.newaxis], xs]
建立模型:
lstm = Sequential()
添加LSTM层:
lstm.add(LSTM(
batch_input_shape=(BATCH_SIZE, TIME_STEPS, INPUT_SIZE),
input_length=TIME_STEPS,
output_dim=CELL_SIZE,
return_sequences=True,
stateful=True
))
添加TimeDistributed输出层:
lstm.add(TimeDistributed(Dense(OUTPUT_SIZE)))
定义优化器:
adam = Adam(LR)
编译:
lstm.compile(optimizer=adam,loss='mse')
训练:
for step in range(501):
X_batch, Y_batch, xs = get_batch()
cost = model.train_on_batch(X_batch, Y_batch)
pred = model.predict(X_batch, BATCH_SIZE)
plt.plot(xs[0, :], Y_batch[0].flatten(), 'r', xs[0, :], pred.flatten()[:TIME_STEPS], 'b--')
plt.ylim((-1.2, 1.2))
plt.draw()
plt.pause(0.1)
if step % 10 == 0:
print('train cost: ', cost)
[TOP]